Effect Of Change In Rotor Resistance On Torque
It is shown that in slip ring induction motor, externally resistance can be added in the rotor. Let us see the effect of change in rotor resistance on the torque produced.
Let R2 = Rotor resistance per phase
Corresponding torque, T α (s E22 R2)/√(R22 +(s X2)2)
Now externally resistance is added in each phase of rotor through slip rings.
Let R2‘ = New rotor resistance per phase
Corresponding torque T‘ α (s E22 R2‘ )/√(R2‘2 +(s X2)2)
Similarly the starting torque at s = 1 for R2 and R2‘ can be written as
Tst α (E22 R2 )/√(R22 +(X2)2)
and T‘st α (E22 R‘2 )/√(R‘22 +(X2)2)
Maximum torque Tm α (E22)/(2X2)
Key Point : It can be observed that Tm is independent of R2 hence whatever may be the rotor resistance, maximum torque produced never change but the slip and speed at which it occurs depends on
R2.
For R2, sm = R2/X2 where Tm occurs
For R2‘, sm‘ = R2‘/X2‘ where same Tm occurs
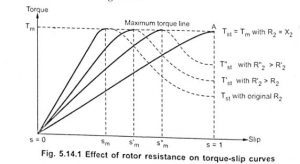
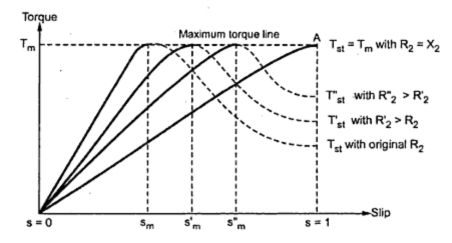
As R2‘ > R2, the slip sm‘ > sm. Due to this, we get a new torque-slip characteristics for rotor resistance . This new characteristics is parallel to the characteristics for with same but Tm occurring at sm‘. The effect of change in rotor resistance on torque-slip characteristics shown in the Fig. 1.
It can be seen that the starting torque T‘st for R2‘ is more than Tst for R2. Thus by changing rotor resistance the starting torque can be controlled.
If now resistance is further added to rotor to get resistance as R2‘ and so on, it can be seen that Tm remains same but slip at which it occurs increases to sm‘ and so on. Similarly starting torque also increases to T‘st and so on.
 |
| Fig. 1 Effect of rotor resistance on torque-slip curves |
If maximum torque Tm is required at start then sm = 1 as at start slip is always unity, so
sm = R2/X2 = 1
R2 = X2 Condition for getting Tst = Tm
Key Point : Thus by adding external resistance to rotor till it becomes equal to X2, the maximum torque can be achieved at start.
It is represented by point A in the Fig. 1.
If such high resistance is kept permanently in the circuit, there will be large copper losses (I2 R) and hence efficiency of the motor will be very poor. Hence such added resistance is cut-off gradually and finally removed from the rotor circuit, in the normal running condition of the motor. So this method is used in practice to achieve higher starting torque hence resistance in rotor is added only at start.
Thus good performance at start and in the running condition is ensured.
Key Point : This is possible only in case of slip type of induction motor as in squirrel cage due to short circuited rotor, extra rotor resistance can not be added.
Example : Rotor resistance and standstill reactance per phase of a 3 phase induction motor are 0.04 Ω and 0.2 Ω respectively. What should be the external resistance required at start in rotor circuit to obtain.
i) maximum torque at start ii) 50% of maximum torque at start.
Solution :
R2 = 0.04 Ω, X2 = 0.2 Ω
i) For Tm = Tst , sm = R2‘/X2 = 1
... R2‘ = X2 = 0.2
Let Rex = external resistance required in rotor.
R2‘ = R2 + Rex
... Rex = R2‘ – R2 = 0.2 – 0.04 = 0.16 Ω per phase
ii) For Tst = 0.5 Tm,
Now Tm= (k E22)/(2 X2) and
Tst = (k E22 R2)/(R22 + X22)
But at start, external resistance Rex is added. So new value of rotor resistance is say R2‘.
R2‘ = R2 + Rex
... Tst = (k E22 R2‘)/(R2‘2 + X22) with added resistance
but Tst = 0.5Tm required.
Substituting expressions of Tst and Tm, we get
(k E22 R2‘)/(R2‘2 + X22) = 0.5 (k E22)/ (2X2)
... 4 R2‘ X2= (R2‘2 + X22)
... (R2‘2) – 4 x 0.2 x R2‘ + 0.22 = 0
... (R2‘2) – 0.8 R2‘ + 0.04 = 0
... R2‘ = {0.8 + √(0.82 – 4 x 0.04)}/2
... R2‘ = 0.0535 , 0.7464 Ω
But R2‘ can not greater than X2 hence,
R2‘ = 0.0535 = R2 + Rex
... 0.0535 = 0.04 + Rex
... Rex = 0.0135 Ω per phase
This is much resistance is required in the rotor externally to obtain Tst = 0.5 Tm.