Three Phase Induction Motor
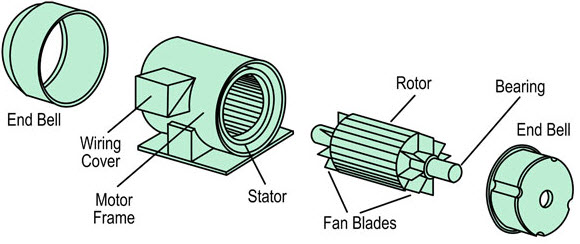
1.Introduction
An electric motor is a device which converts an electrical energy into a mechanical energy. The motors operating on a.c. supply are called a.c. motor. As a.c. supply is commonly available, the a.c. motors are very popularly used in practice. The a.c. motors are classified as three phase induction motors, single phase induction motor, universal motors, synchronous motors etc. The three phase induction motors are widely used for various industrial application. The important features of three phase induction motors are self starting, higher power factor, good speed regulation and robust construction. This chapter explains the construction, working principle and characteristics of three phase induction motors as well as universal motors. The working of three phase induction motors is based on the principle of rotating magnetic field. Let us discuss, the production of rotating magnetic field.
2. Rotating Magnetic field (R.M.F.)
The rotating magnetic field can be defined as the field or flux having constant amplitude but whose axis is continuously rotating in a plane with a certain speed. So if the arrangement is made to rotate a permanent magnet, then the resulting field is a rotating magnetic field. But ion this method, it is necessary to rotate a magnet physically to produce rotating magnetic field.
But in three phase induction motors such a rotating magnetic field is produced by supplying currents to a set of stationary windings, with the help of three phase a.c. supply. The current carrying windings produce the magnetic field or flux. And due to interaction of three phase fluxes produced due to three phase supply, resultant flux has a constant magnitude and its axis rotating in space, without physically rotating the windings. This type of field is nothing but rotating magnetic field. Let us study how it happens.
2.1 Production of R.M.F.
A three phase induction motor consists of three phase winding as its stationary part called stator. The three phase stator winding is connected in star or delta. The three phase windings are displaced from each other by 120o. The windings are supplied by a balanced three phase a.c. supply. This is shown in the Fig. 1. The three phase windings are denoted as R-R’ , Y-Y’ and B-B’.
 |
| Fig. 1 Star or delta connected 3phase winding |
The three phase currents flow simultaneously through the windings and are displaced from each other by 120o electrical. Each alternating phase current produces its own flux which is sinusoidal. So all three fluxes are sinusoidal and are separated from each other by 120o. If the phase sequence of the windings is R-Y-B, then mathematical equations for the instantaneous values of the three fluxes ΦR , ΦY and ΦB can be written as,
ΦR = Φm sin(Φt) = Φm sin Φ ………..(1)
ΦY = sin (Φt – 120o) = Φm sin (Φ – 120o) …………(2)
ΦB = Φm sin (Φt – 240o) = Φm sin (Φ – 240o) ………….(3)
As winding are identical and supply is balanced, the magnitude of each flux is Φm. Due to phase sequence R-Y-B, flux lags behind ΦR by 120o and ΦB lags ΦY by 120o. So ΦB ultimately lags ΦR by 240o. The flux ΦR is taken as reference while writing the equations.
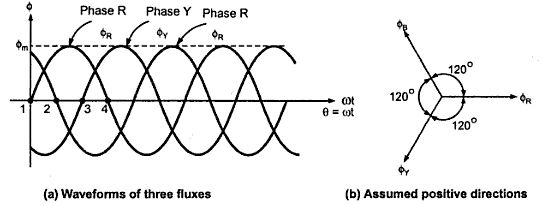
The Fig. 2(a) shows the waveforms of three fluxes in space. The Fig.2(b) shows the phasor diagram which clearly shows the assumed positive directions of each flux. Assumed positive direction means whenever the flux is positive it must be represented along the direction shown and whenever the flux is negative it must be represented along the opposite direction to the assumed positive direction.
Let ΦR, ΦY and ΦB be the instantaneous values of the three fluxes. The resultant flux ΦT is the phasor addition of ΦR, ΦY and ΦB.
Let us find ΦT at the instants 1, 2, 3 and 4 as shown in the Fig. 2(a) which represents the values of Φ as 0o, 60o, 120o and 180o respectively. The phasor addition can be performed by obtaining the values of ΦR, ΦY and ΦB by substituting values of Φ in the equation (1), (2) and (3).
 |
| Fig. 2 |
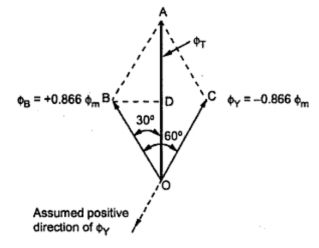
Case 1 : Φ = 0o
Substituting in the equations (1), (2) and (3) we get,
ΦR = Φm sin 0o = 0
ΦY = Φm sin(-120o ) = -0.866 Φm
ΦB = Φm sin (-240o) = + 0.866 Φm
 |
| Fig. 3(a) Vector diagram of Φ = 0o |
The pahsor addition is shown in the Fig. 3(a). The positive values are are shown in assumed positive directions while negative values are shown in opposite direction to the assumed positive directions of the respective fluxes. Refer to assumed positive directions shown in the Fig 3(b).
BD is drawn perpendicular from B on ΦT. It bisects ΦT.
... OD = DA = ΦT/2
In triangle ΦOBD = 30o
... cos 30o = OD/OB = (ΦT/2)/(0.866 Φm )
... ΦT = 2 x 0.866 Φm x cos 30o
= 1.5 Φm
So magnitude of ΦT is 1.5 Φm and its position is vertically upwards at Φ = 0o.
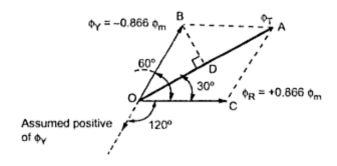
Case 2 Φ = 60o
Equation (1),(2) and (3) give us,
ΦR = Φm sin 60o = +0.866 Φm
ΦY = Φm sin (-60o) = -0866 Φm
ΦB = Φm sin (-180o) = 0
So ΦR is positive and ΦY is negative and hence drawing in appropriate directions we get phasor diagram as shown in the Fig. 3(b).
 |
| Fig 3(b) Vector diagram of Φ = 60o |
Doing the same construction, drawing perpendicular from B on at D we get the same result as,
ΦT = 1.5 Φm
But it can be seen that though its magnitude is 1.5 Φm it has rotated through 60o in space, in clockwise direction, from its previous position.
Case 3 : Φ = 120o
Equations (1),(2) and (3) give us,
ΦR = Φm sin 120o = +0.866 Φm
ΦY = Φm sin 0o = 0
ΦB = Φm sin (-120o ) = -0.866 Φm
So ΦR is positive and ΦB is negative. showing ΦR and ΦB in the appropriate directions, we get the phasor diagram as shown in the Fig . 3(c).
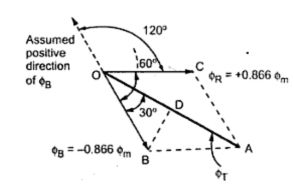 |
| Fig. 3(c) Vector diagram of Φ = 120o |
After doing the construction same as before i.e. drawing perpendicular from B on ΦT, it can be provided again that, ΦT = 1.5 Φm
But the position of ΦT is such that it has rotated further through 60o from its previous position, in clockwise direction. And from its position at Φ = 0o, it has rotated through 120o in space, in clockwise direction.
Case 4 : Φ = 180o
From equations (1),(2) and (3),
ΦR = Φm sin (180o) = 0
ΦY = Φm sin (60o) = +0.866 Φm
ΦB = Φm sin (-60o)
= -0.866 Φm
 |
| Fig. 3(d) Vector diagram of Φ = 180o |
So ΦR = 0 , ΦY is positive and ΦB is negative. Drawing ΦY and ΦB in the appropriate directions, we get the phasor diagram as shown in the Fig. 3(d).
From phasor diagram, it can be easily proved that,
ΦT = 1.5 Φm
Thus the magnitude of ΦT once again remains same. But it can be seen that it has further rotated through 60o from its previous position in clockwise direction.
So for an electrical half cycle of 180o, the resultant ΦT has also rotated through . This is applicable for the windings from the above discussion we have following conclusions :
a)
The resultant of the three alternating fluxes, separated from each
other by , has a constant amplitude of 1.5 Φm where Φm is maximum
amplitude of an individual flux due to any phase.
b) The resultant always keeps on rotating with a certain speed in space.
Key point :
This shows that when a three phase stationary windings are excited by balanced three phase a.c. supply then the resulting field produced is rotating magnetic field. Though nothing is physically rotating, the field produced is rotating in space having constant amplitude.
2.2 Speed of R.M.F.
There exists a fixed relation between frequency f of a.c. supply to the windings, the number of poles P for which winding is wound and speed N r.p.m. of rotating magnetic field. For a standard frequency whatever speed of R.M.F. results is called synchronous speed, in case of induction motors. It is denoted as .
![]()
= (120 f)/P = speed of R.M.F.Where f = Supply frequency in Hz
p = Number of poles for which winding is wound
This is the speed which R.M.F rotates in space. Let us see how to change direction of rotation of R.M.F.2.3 Direction of R.M.F.
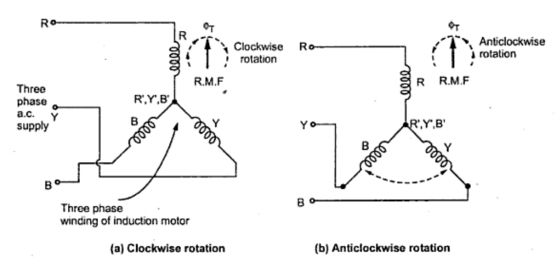 |
| Fig. 4 |
The direction of the R.M.F. is always from the axis of the leading phase of the three phase winding towards the lagging phase of the winding. In a phase sequence of R-Y-B, phase R leads Y by 120o and Y leads B by120o. So R.M.F. rotates from axis of R to axis of Y and then to axis of B and so on. So its direction is clockwise as shown in the Fig. 4(a). This direction can be reversed by interchanging any two terminals of the three phase windings while connecting to the three phase supply. The terminals Y and B are shown interchanged in the Fig. 4(b). In such case the direction of R.M.F. will be anticlockwise.
As Y and B of windings are connected to B and Y from winding point of view the phase sequence becomes R-Y-B. Thus R.M.F. axis follows the direction from R to B to Y which is anticlockwise.
Key point :
Thus by interchanging any two terminals of three phase winding while connecting it to three phase a.c. supply, direction of rotation of R.M.F. gets reversed.