Condition Of Maximum Torque In Three Phase Induction Motor
From the torque equation, it is clear that torque depends on slip at which motor is running. The supply voltage to the motor is usually rated and constant and there exists a fixed ratio between E1 and E2. ence E2 is also consatnt. Similarly R2, X2 and ns are constants for the induction motor.
Hence while finding the condition for maximum torque, remember that the only parameter which controls the torque is slip s.
Mathematically for the maximum torque we can write,
dT/ds = 0
where T = (k s E22 R2)/(R22 +(s X2)2)
While carrying out differential remember that E2, R2, X2 and k are constants. The only variable is slip s. As load on motor changes, its speed changes and hence slip changes. This slip decides the torque produced corresponding to the load demand.
T = (k s E22 R2)/(R22 + s2 X22) …….Writing (s X2)2 = s2 X22
As both numerator and denominator contains s terms, differential T with respect to s using the rule of differentiation for u/v.
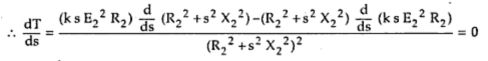
.. k s E22 R2 (2s X22) – (R22 + s2 X22)(k E22 R2) = 0
... 2 s2 k X22 E22 R2 – R22 k E22 R2 – k s2 X22 E22 R2 = 0
... k s2 X22 E22 R2 – R22 k X22 R2 = 0
... s2 X22 – R22 = 0 Taking k E22 R2 common.
... s2 = R22/X22
... s = R2/X2 Neglecting negative slip
This is the slip at which the torque is maximum and is denoted as sm.
... sm= R2/X2
It is the ratio of standstill per values values of resistance and reactance of rotor, when the torque produced by the induction motor is at its maximum.
1.1 Magnitude of Maximum Torque
This can be obtained by substituting sm = R2/X2 in the torque equation. It is denoted by Tm.
Tm = (k sm E22 R2)/(R22 +(sm X2)2)
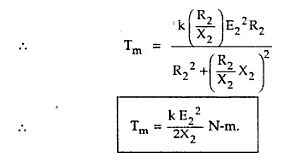
From the expression of Tm, it can be observed that
1. It is inversely proportional to the rotor reactance.
2. It is directly proportional to the square of the rotor induced e.m.f. at standstill.
3. The most interesting observation is, the maximum torque is not dependent on the rotor resistance R2.
But the slip at which it occurs i.e. speed at which it occurs depends on the value of rotor resistance R2.
Example 1 : A 400 V, 4 pole, 3 phase, 50 Hz star connected induction motor has a rotor resistance and reactance per phase equal to 0.01 Ω and 0.1 Ω respectively. Determine i) Starting torque ii) slip at which maximum torque will occur iii) speed at which maximum torque will occur iv) maximum torque v) full load torque if full load slip is 4 %. Assume ratio of stator to rotor turns as 4.
Solution : The given values are,
P = 4, f = 50 Hz, stator turns/ rotor turns = 4, R2 = 0.01 Ω, X2 = 0.1 Ω
E1line = stator line voltage = 400 V
E1ph = E1line/√3 = 400/√3 = 230.94 V …………star connection
K = E2ph/E1ph = Rotor turns/ Stator turns = 1/4
... E2 = (1/4) x E1ph = 230.94/4 = 57.735 V
Ns = 120f/P = 120×50 / 4 = 1500 r.p.m.
i) At start, s =1
... Tst = (k E22 R2)/(R22 +( X2)2) where k = 3/(2 π ns)
ns = Ns/60 = 1500/60 = 25 r.p.s.
... k = 3/(2π x 25) = 0.01909
... Tst = ( 0.01909 x 57.7352 x 0.01 )/( 0.012 + 0.12 ) = 63.031 N-m
ii) Slip at which maximum torque occurs is,
sm = R2/X2 = 0.01/0.1 = 0.1
%sm = 0.1 x 100 = 10%
iii) Speed at which maximum torque occurs is speed corresponding to,
N = Ns (1 – sm ) = 1500 (1 – 0.1) = 1350 r.p.m.
iv) The maximum torque is,
Tm = (k E22)/(2 X2) = (0.01909 x 57.7352)/(2 x 0.1) = 318.16 N-m
v) Full load slip, sf = 0.04 as % sf = 4 %
... Tf.l. = (k sf E22 R2)/(R22 +(sf X2)2) = (0.01909 x 0.04 x 57.7352 x 0.01)/( 0.012 + (0.04 x 0.1)2)
= 219.52 N-m