Exact Voltage Drop
In Figure 1.40, the exact voltage drop is AH instead of AG. During calculation of approximate voltage drop, AG has already been calculated. If GH is being added to AG, the exact voltage drop can be obtained.
Consider the right-angled triangle OCG. We have
OC2 = OG2 + GC2
i.e. OC2 – OG2 = GC2
i.e. (OC – OG)(OC + OG) = GC2
i.e. (OH –OG)(OC + OG) = GC2
i.e. GH.2.OC= GC2 [Taking OC ≍ OG]
i.e. 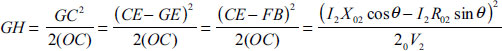
For lagging power factor, the exact voltage drop is
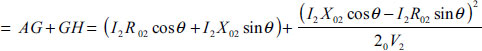
For leading power factor, the exact voltage drop is given by
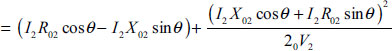
In general, the voltage drop is
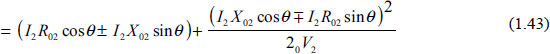
and percentage voltage drop is
![]()
![]()
It may be noted that the upper sign is to be used for lagging power factor and the lower sign for leading power factor.
Example 1.11 The OC and SC tests on a 300/600 V, 50 Hz, single-phase transformer gave the fol-lowing results:
OC test (LV side): 300 V, 0.8 A, 70 W
SC test (HV side): 20 V, 12 A, 90 W
where LV and HV is low voltage and high voltage, respectively.
Find the equivalent circuit of the transformer referred to as LV side and also calculate the secondary voltage when delivering 6 kW at 0.8 p.f. (power factor) lagging.
Solution
OC test (LVside):
Instruments are placed on LV side and HV side is kept open.
V1 = 300 V, I0 = 0.8 A, W0 = 70 W
Now, ![]()
∴ IW= I0cosθ0=0.8×0.292=0.2336A
and Iμ=I0sinθ0=0.8×0.956=0.7648A
∴ ![]()
SC test:
Instruments are placed on HV side and LV side is kept open.
![]()
VSC = 20 V, ISC = 12 A, PSC = 90 W
![]()
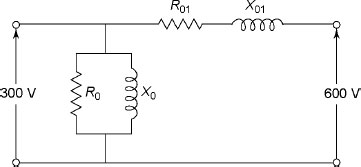 Figure E1.2
Figure E1.2
∴![]()
∴![]()
∴![]()
∴![]()
The equivalent circuit referred to as LV side is shown in Figure E1.2.
∴ ![]()
Approximate voltage drop referred to as secondary for 0.8 power factor lagging is
=I2(R02cosθ+X02sinθ
=12.5×(0.625×0.8+1.548×0.6)=17.86 V
∴ Secondary terminal voltage = 600 – 17.86 = 582.14 V (approx.)