Basic Terms In Electrical Machine
INDUCED EMF
An emf is induced in the conductor either (i) dynamically or (ii) statically. In the first case, the conductor will move in the magnetic field and the flux will be non-varying. In the second case, the conductor will be stationary and the flux will be varying.
Dynamically Induced emf
In Figure 12(a), conductor A is shown by the cross-section within the uniform magnetic field. It moves at the right angle to the magnetic field of flux density B Wb/m2. If the conductor moves a length dx in time dt, the area swept by it is equal to Idx, where l is the length of the conductor lying within the magnetic field. Here, change in flux is equal to Bldx in time dt. According to Faraday’s law, the induced emf (also known as dynamically induced emf) is expressed as
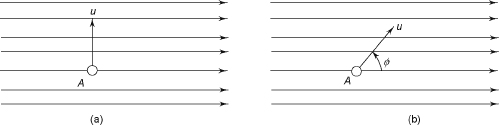
Figure 12 Dynamically Induced emf
where 
= the velocity of the conductor if the conductor moves at an angle Φ with the magnetic field shown in Figure 12(b). The component of its velocity in the direction perpendicular to the field is u sin Φ. The induced emf (e) becomes
If the conductor moves parallel to the field, the value of Φ will be 0°. The induced emf becomes zero; i.e., e = 0.
The direction of the induced emf can be found out by Fleming’s right-hand rule as shown in Figure 13. This rule states that if anyone spreads the thumb, forefinger and second finger of the right hand so that they are mutually perpendicular to each other, the thumb indicates the direction of rotation of the conductor in the magnetic field, the forefinger shows the direction of the magnetic field and the second finger indicates the direction of the flow of the induced current in the conductor.
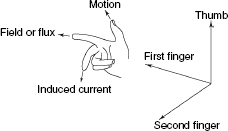
Figure 13 Fleming’s Right-hand Rule
DC generators work on the principle of production of dynamically induced emf in the conductors, which are housed in a revolving armature lying within the magnetic field.
Statically Induced emf
If the flux in coil A varies by varying current with the help of the rheostat, the flux linked with coil Balso changes and emf is induced in coil B, and its direction will be obtained by Lenz’s law.
Coil A is connected to a battery (E) via a rheostat (Rh) as shown in Figure 14. Coil B is connected to a voltmeter (V). When the current in coil A is established, the flux will be produced in coil A, and it varies by varying the current in the coil with the help of the rheostat. This varying flux links with coil B and emf is induced in the coil. This emf is also called mutually induced emf. In this case there is no movement of coil B. Similarly, if the connection is reversed, that is, a voltmeter is connected to coil Aand the battery and the rheostat to coil B, the emf will be produced in coil A.
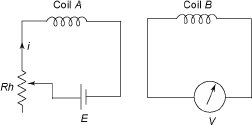
Figure 14 Statically Induced emf in Coil B due to Variation of Flux in Coil A
Another type of statically induced emf in a coil is the self-induced emf in a coil, which is produced due to the changes of flux in the coil itself by changing the current through it. In Figure 15, the current through the coil is changed by the rheostat (Rh). The flux linked with the coil also changes producing self-induced emf in the coil. The direction of the induced emf in the coil is obtained by Lenz’s law that opposes any change of flux in it. This emf is also known as opposing emf or counter emf.
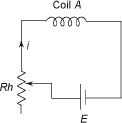
Figure 15 Statically Induced emf in a Single Coil
MAGNETIC CIRCUITS
Magnetic flux lines form closed loops. A magnetic circuit is defined as the closed path followed by flux lines. An electric circuit provides a path for electric current, whereas a magnetic circuit provides a path for magnetic flux. The knowledge of magnetic circuits is of utmost importance in the design, analysis and applications of electromagnetic devices such as transformers, rotating electrical machines and electromagnetic relays. The basics of magnetic circuits are introduced in the following sections.
MAGNETOMOTIVE FORCE
A current-carrying conductor produces a magnetic field around it. The coil should have the correct number of turns in order to produce the required flux density. Magnetomotive force (mmf) is defined as the product of current and number of turns.
Magnetomotive force = Current × Turns
Let I be the current through the coil (A) and N be the number of turns in the coil.
The unit of mmf is ampere-turns (AT). Since N is dimensionless, its unit is ampere (A) also.
MAGNETIC FIELD INTENSITY
Magnetomotive force per unit length of magnetic flux path is called magnetic field intensity (H).
where l is the mean length of the magnetic circuit in metres. Magnetic field intensity is also called magnetic field strength or magnetizing force.
From Equation (5),
MAGNETIC FLUX
A current-carrying conductor produces a magnetic field around it. The magnetic field is measured in terms of flux lines (or simply flux) Φ and flux density B, the number of flux lines per unit area.
The density of flux is greatest near the conductor and tapers off inversely with distance.
The unit of flux Φ is webers (Wb) and the unit of magnetic intensity (B) is webers per metre square (Wb/ m2) or tesla (T).
1 weber = 108
1 gauss = 1 Wb/cm2 = 10-4 Wb/m2
1 tesla = 104 gausses
These units are in rationalized MKS system.
By Ampere’s law, the line integral of the field intensity 
around a closed path is equal to the current enclosed by that path.
The line integral of the closed path dl is the circumference of the circle 2πr.
From Equation (8),
From Equation (9) and (10),
i.e., 
For medium other than free space,
μ = μ0μr
where μr is the relative permeability.
Flux is produced by current
Φ∝I.
If there are N turns instead of single conductor,
where NI, called ampere-turns (AT), is the flux-producing ability of the current-carrying circuit.
We can visualize NI or AT as the force that produces flux and hence is called the magnetomotive force, mmf (F).
Thus, we have arrived at a magnetic circuit similar to an electric circuit.
The medium surrounding the conductor causes resistance to the creation of flux. In the magnetic circuit, this resistance is called reluctance (S).
where S is the reluctance.
As in the case of an electric circuit, reluctance is directly proportional to length, l and inversely to area, A, and the property of the material called permeability, μ.
So, higher the permeability, lesser the reluctance and greater the flux.
We have seen that permeability of free space is very low, 4π × 10-7 H/m. Ferromagnetic materials, that is, alloys of iron with cobalt, tungsten, nickel and aluminum, have very high permeability (μr), ranging from 2,000 to 80,000. High-permeability materials have the property of confining the flux within their cross-sectional area instead of spreading out as in space.