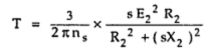Relation Between P2, Pc, And Pm
The rotor input P2, rotor copper loss Pc and gross mechanical power developed Pm are related through the slip s. Let us derive this relationship.
Let T = Gross torque developed by motor in N-m.
We know that the torque and power are related by the relation,
P = T x ?
where P = Power
and ? = angular speed
= (2?N)/60 , N = speed in r.p.m.
Now input to the rotor P2 is from stator side through rotating magnetic field which is rotating at synchronous speed Ns.
So torque developed by the rotor can be expressed interms of power input and angular speed at which power is inputted i.e. ?s as,
P2 = T x ?s where ?s = (2?Ns)/60 rad/sec
P2 = T x (2?Ns)/60 where Ns is in r.p.m. ………..(1)
The rotor tries to deliver this torque to the load. So rotor output is gross mechanical power developed Pm and torque T. But rotor gives output at speed N and not Ns. So from output side Pm and T can be related through angular speed ? and not ?s.
Pm= T x ? where ? = (2?N)/60
Pm = T x (2?N)/60 ………….(2)
The difference between P2 and Pm is rotor copper loss Pc.
Pc = P2 – Pm = T x (2?Ns/60) – T x (2?N/60)
Pc = T x (2?/60)(Ns – N) = rotor copper loss ………..(3)
Dividing (3) by (1),
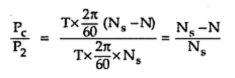
Pc/P2 = s as (Ns – N)/Ns = slip s
Rotor copper loss Pc = s x Rotor input P2
Thus total rotor copper loss is slip times the rotor input.
Now P2 – Pc = Pm
P2 – sP2 = Pm
(1 – s)P2 = Pm
Thus gross mechanical power developed is (1 – s) times the rotor input
The relationship can be expressed in the ratio from as,

The ratio of any two quantities on left hand side is same as the ratio of corresponding two sides on the right hand side.
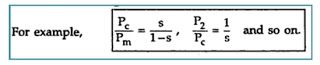
This relationship is very important and very frequently required to solve the problems on the power flow diagram.
Key Point :
The torque produced by rotor is gross mechanical torque and due to mechanical losses entire torque can not be available to drive load. The load torque is net output torque called shaft torque or useful torque and is denoted as Tsh. It is related to Pout as,

and Tsh < T due to mechanical losses.
1.1 Derivation of k in Torque Equation
We have seen earlier that
T = (k s E22 R2)/(R22 +(s X2)2)
and it mentioned that k = 3/(2? ns) . Let us see its proof.
The rotor copper losses can be expressed as,
Pc = 3 x I2r2 x R2
but I2r = (s E2)/?(R22 +(s X2)2), hence substituting above
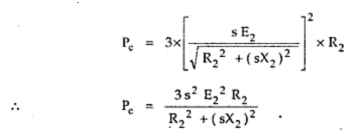
Now as per P2 : Pc : Pm is 1 : s : 1-s ,
Pc/Pm = s/(1-s)
Now Pm = T x ?
= T x (2?N/60)
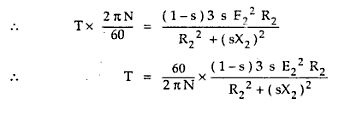
Now N = Ns (1-s) from definition of slip, substituting in above,
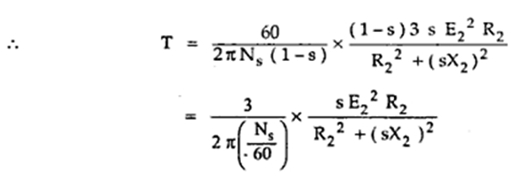
but Ns/60 = ns in r.p.m.
So substituting in the above equation,